Фрагменты семинара по теме "Специальные представления БФ" от 28 февраля

1) На снимке видны:

• формулы для представления в виде СДНФ и СКНФ и

• примеры представления БФ двух и трёх переменных в виде СДНФ и СКНФ

2) На снимке дан пример представления импликации в виде полинома Жегалкина первым методом ("через СДНФ")

3) На следующих двух снимках даны примеры представления заданных графически БФ трёх переменных в виде полинома Жегалкина вторым методом (методом "неопределенных коэффициентов")

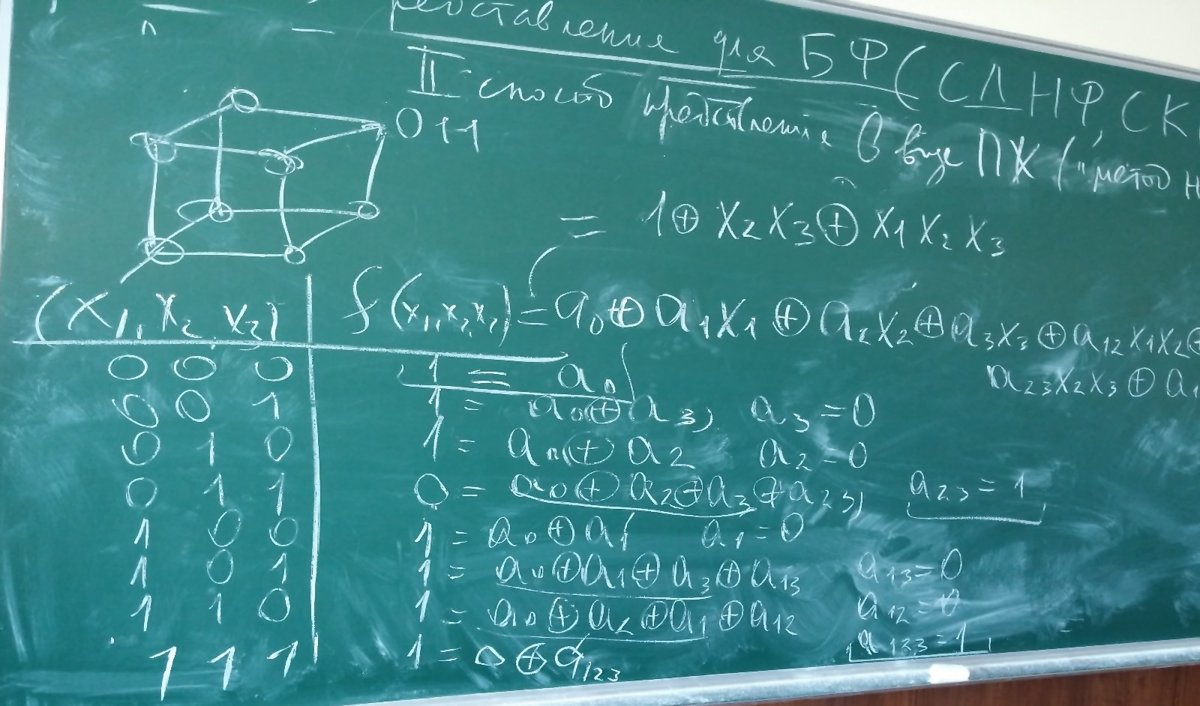
Примеры представления в виде полинома Жегалкина БФ от трёх переменных первым и вторым способом:

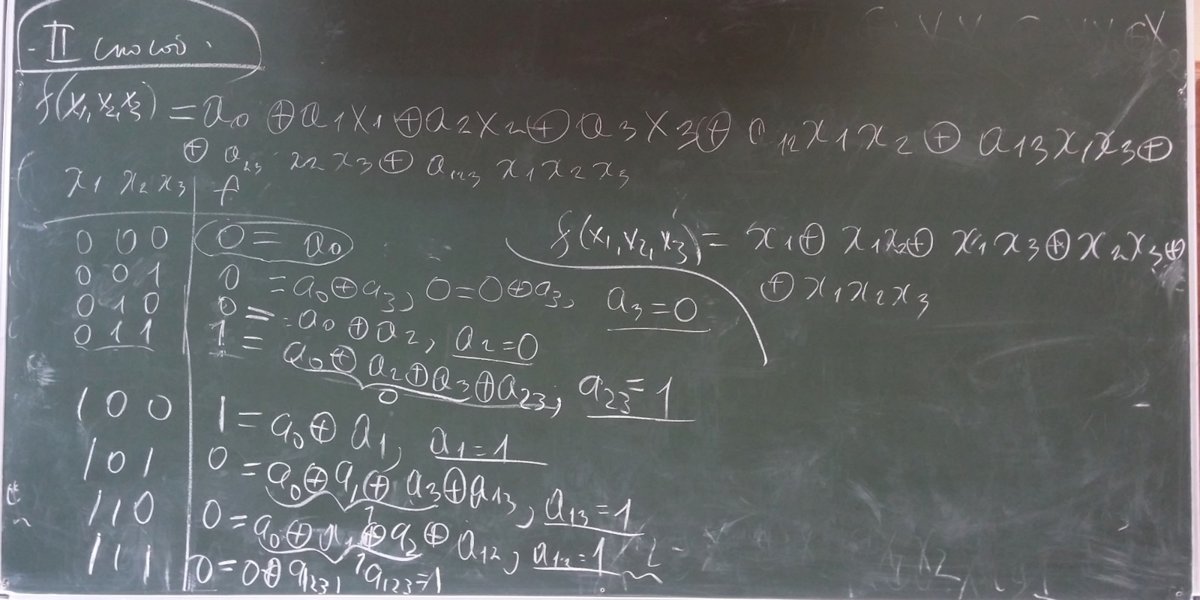
Фрагменты семинаров от 7, 14 и 15 марта

Пример минимизации булевой функции 4-х переменных (метод Карно), в котором минимальная ДНФ единственна.

На следующих двух снимках представлены:
а) общая концепция геометрического подхода, при котором отыскание для заданной функции ДНФ минимального ранга сводится к отысканию покрытия минимального ранга для носителя функции с помощью максимальных интервалов;
б) последовательная классификация интервалов для заданной функции;
в) примеры построения покрытий ядрового и минимального.

Пример минимизации булевой функции 4-х переменных (метод Карно), в котором существует два варианта ДНФ минимальной.

Пример минимизации булевой функции 3-х переменных (геометрический метод): последовательно найдены ДНФ сокращённая, ДНФ ядровая и два варианта ДНФ минимальной.

Пример минимизации булевой функции 3-х переменных, заданной векторным способом, (геометрический метод): совпадают ДНФ сокращённая, ДНФ ядровая и ДНФ минимальная.
На самом начальном этапе осуществляется геометрическое задание функции -- исходное для применения геометрического метода.

Домашнее задание: минимизировать три функции 4-х переменных, заданные векторным способом.
Для первой функции f(x_1,x_2,x_3,x_4) минимизация начата, но не закончена: последовательно найдены ДНФ сокращённая, ДНФ ядровая и два варианта ДНФ минимальной, но не выписаны точно (через переменные x_1,x_2,x_3 и x_4) простые импликанты K_1,...., K_5.
Закончить минимизацию для функции f и провести самостоятельно минимизацию для функций g и h.

Решение задач на минимизацию БФ на лекциях и семинарах от 21 и 22 марта

Использование функции Патрика для отыскания минимальных ДНФ (простой пример).

Решение задачи на минимизацию БФ методом Квайна-Маккласки.

Использование функции Патрика для отыскания минимальных ДНФ (сложный пример). Под многоточием скрыты слагаемые, которые дают тупиковые ДНФ, не являющиеся минимальными. Все минимальные ДНФ порождаются выписанными членами.

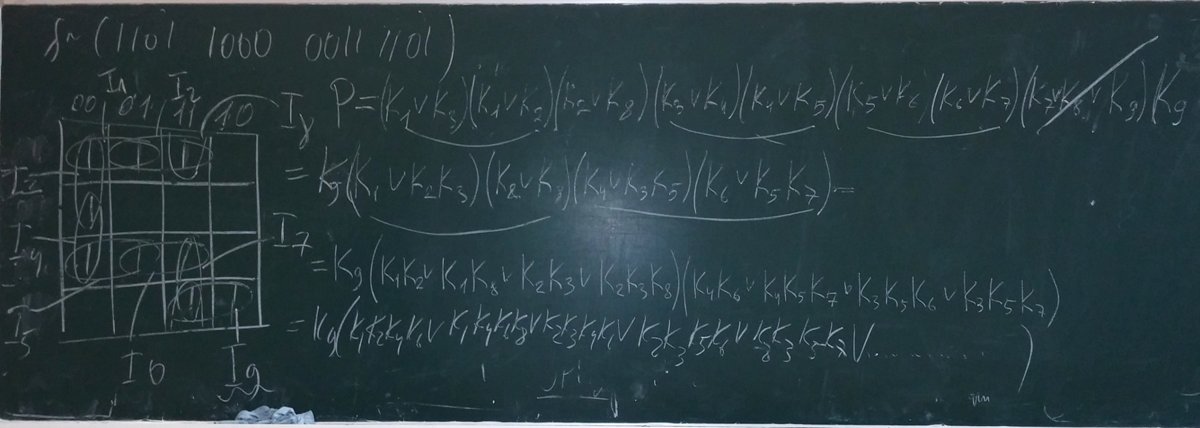
Решение задачи на минимизацию БФ методом Карно.

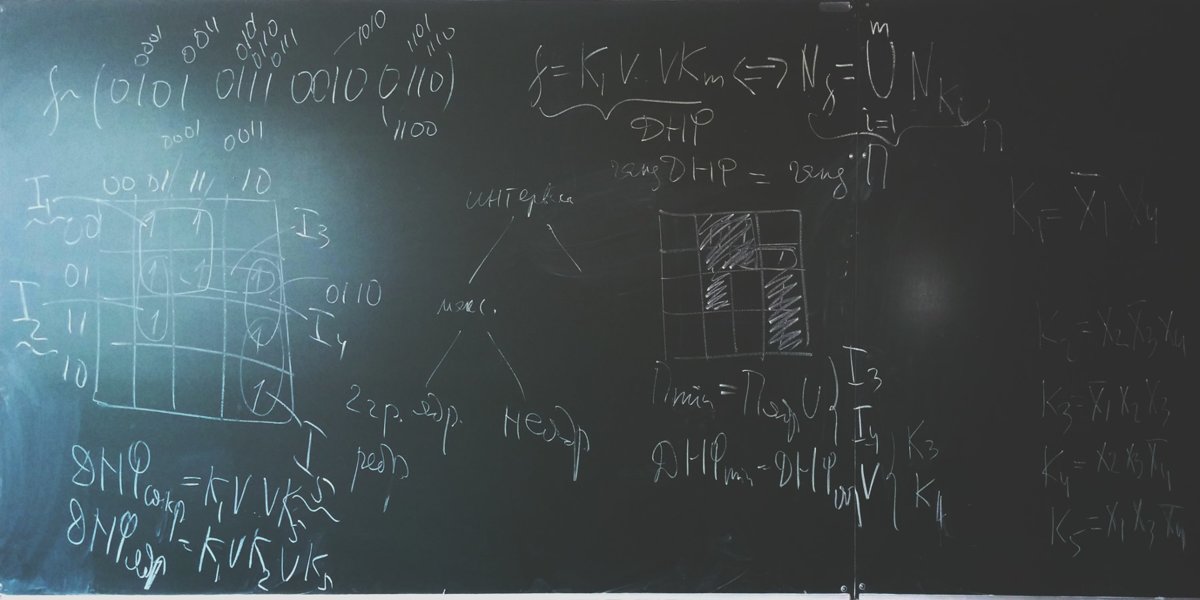
Решение задачи на минимизацию БФ методом Квайна-Маккласки.

Решение задачи на минимизацию БФ методом Карно.


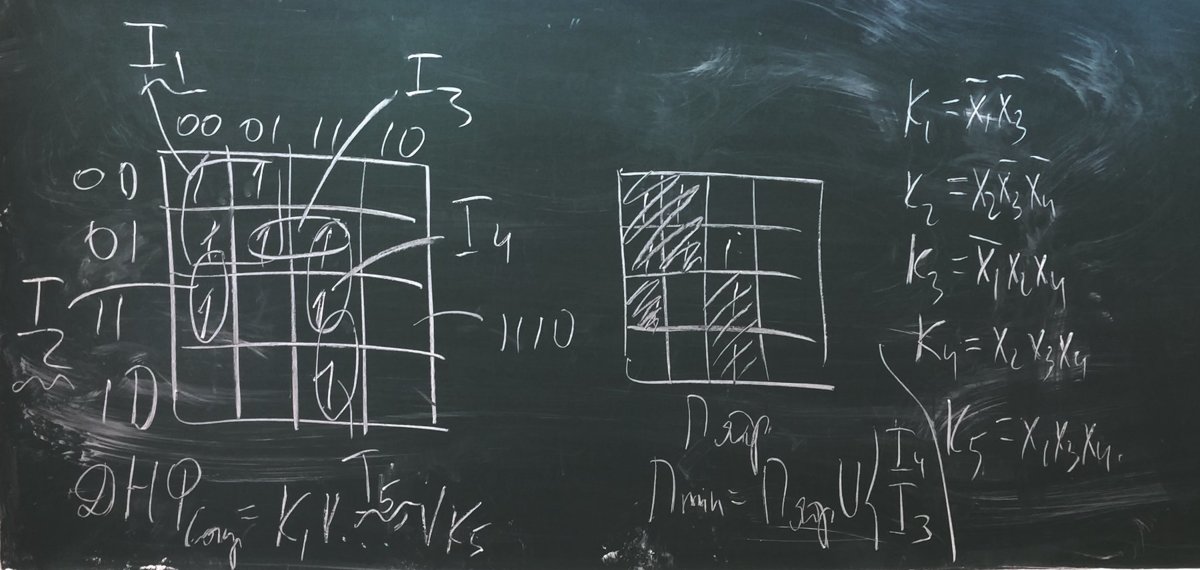
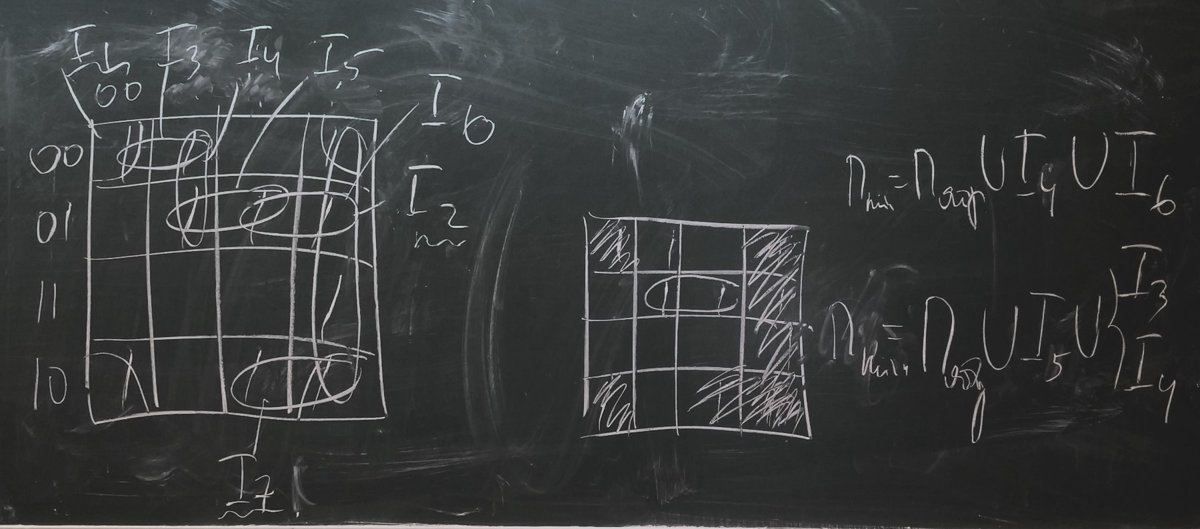
Решение задачи на минимизацию БФ методом Квайна-Маккласки.

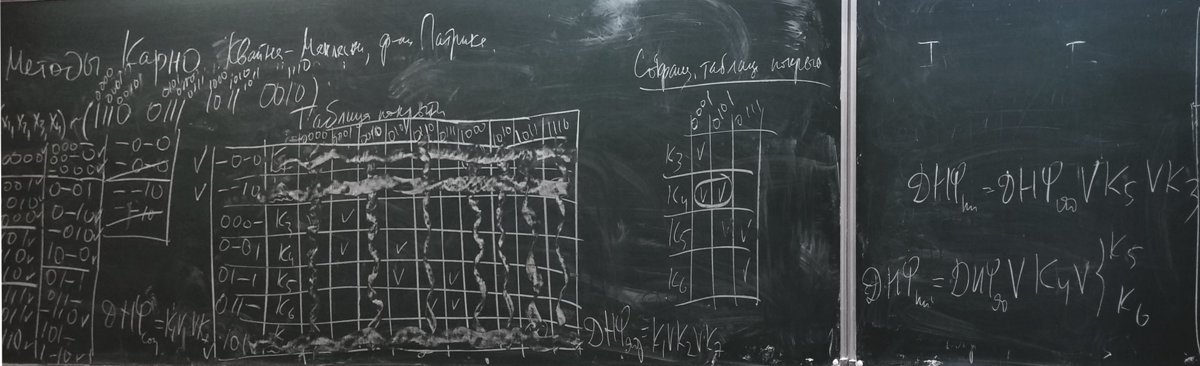
Использование функции Патрика для отыскания минимальных ДНФ

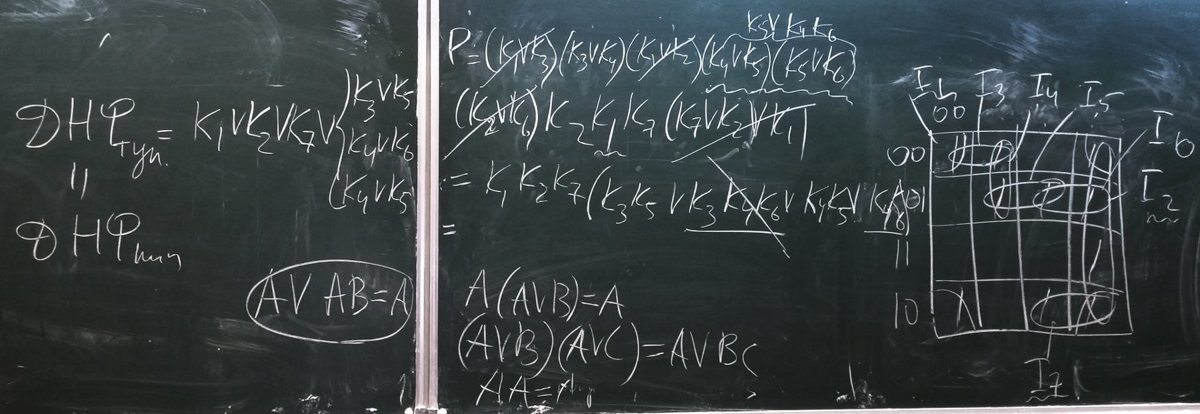
Материалы для подготовки к контрольной работе №1

Задачи на графический метод

Задачи на функцию Патрика

Пример А.
Найти все тупиковые и минимальные ДНФ для булевой функции четырёх переменных, заданной вектором:

1. (0111 1110)
2. (1111 0101)
3. (1101 1011)

Фрагменты семинаров от 4 и 5 апреля

Разбор самостоятельной работы на минимизацию булевых функций геометрическим методом (для функций трёх переменных) и методом Карно (для функций четырёх переменных). В каждом из двух вариантов были заданы векторым способом функции f(x_1,x_2,x_3) и g(x_1,x_2,x_3,x_4)

Разбор задачи: для заданной несамодвойственной функции f(x_1,x_2,x_3) найти все способы получения констант по лемме S

Построение полинома Жегалкина методом неопределённых коэффициентов для заданной нелинейной функции f(x_1,x_2,x_3). Далее -- получение формулы для конъюнкции и дизъюнкции через f(x_1,x_2,x_3) по лемме L.

Решение задачи на получение формулы для отрицания через заданную функцию f(x_1,x_2,x_3) по лемме М всеми возможными способами.

Пример построения полинома Жегалкина через СДНФ. Функция f(x_1,x_2,x_3) задана векторным способом.

Пример сворачивания упрощенного (за счет подстановки константы) полинома Жегалкина к конъюнкции и дизъюнкции.

Фрагменты семинара от 18 апреля

Пример полной системы, состоящей из одной функции f(x_1,x_2,x_3). Демонстрация схем, реализующих основные булевы функции.

Пример полной системы, состоящей из трёх функции f, g и h. Последовательное получения формул для отрицания и констант через функции f, g и h. Демонстрация схем, сопровождающих эти формулы.

Фрагменты семинара от 26 апреля

На правой части доски представлены два изображения транспортной сети.
На верхнем изображении видны этапы постепенной нагрузки ребёр с целью создания максимального потока: первое число на каждом ребре -- пропускная способность ребра, числа после левой круглой скобки -- текущие величины потока на ребре, при этом последнее их них -- окончательная величина потока на ребре. Закрытие круглых скобок означает насыщение ребра. На верхнем изображении указан также минимальный разрез.

На нижнем изображении представлен максимальный поток (без этапов его построения):
первое число на каждом ребре -- пропускная способность ребра, число в скобках -- величина максимального потока на этом ребре. Волнистой линией тут же показан минимальный разрез. Сбоку записаны величина (мощность) максимального потока и пропускная способность минимального разреза. Они равны, что соответствует теореме Форда--Фалкерсона.

На левой части доски представлены два графа перестройки G_1 и G_2, а также соединяющие источник со стоком цепи, по которым шла постепенная нагрузка сети. На первом шаге выбираются две непересекающиеся цепи, на втором шаге -- только одна цепь.

На правой части доски представлены два изображения транспортной сети.
На верхнем изображении видны этапы постепенной нагрузки ребёр с целью создания максимального потока: первое число на каждом ребре -- пропускная способность ребра, числа после левой круглой скобки -- текущие величины потока на ребре, при этом последнее их них -- окончательная величина потока на ребре. Закрытие круглых скобок означает насыщение ребра. На верхнем изображении указан также минимальный разрез.

На нижнем изображении представлен максимальный поток (без этапов его построения): первое число на каждом ребре - пропускная способность ребра, число в скобках -- величина максимального потока на этом ребре. Волнистой линией тут же показан минимальный разрез. Сбоку записаны величина (мощность) максимального потока и пропускная способность минимального разреза. Они равны, что соответствует теореме Форда--Фалкерсона.

На левой части доски представлены три графа перестройки G_1, G_2 и G_3.
В нижней части доски указаны соединяющие источник со стоком цепи, по которым шла постепенная нагрузки сети. На первом шаге выбирается цепь с максимальной пропускной способностью 4, на втором шаге выбираются две непересекающиеся цепи с пропускными способностями 1 и 1, на третьем шаге -- только одна цепь с пропускной способностью 1. Третья цепь содержит реверсное ребро!

Потоковая контрольная работа 10 мая 2017 года (условия задач и примерный вариант)

Задача 1. Найти ДНФ сокращенную, ядровую, минимальные для функций f(x,y,z) и g(x,y,z), используя графический метод.
f~(1111 1100), g~(1010 0011)
Задача 2. Найти ДНФ сокращенную, ядровую, минимальные для функции f(x_1,x_2,x_3,x_4) ), используя метод Карно либо метод Квайна -- Макласки.
f~(1010 0101 1111 0011)
Задача 3. Доказать по теореме Поста полноту системы булевых функций; выразить формулами над этой системой следующие функции: 1, 0, отрицание, конъюнкцию, дизъюнкцию.
S_1={f~(1110 0000)}
Задача 4. Доказать по теореме Поста полноту системы булевых функций; выразить формулами над этой системой следующие функции: 1, 0, отрицание, конъюнкцию, дизъюнкцию.
S_2={f~(1001), g~(0101 0100)}

Задачи с семинара 3 мая

Поточная контрольная работа по теме "Экстремальные задачи на графах"

Примерный вариант:

Фрагменты семинара от 23 мая (подготовка к контрольной работе №2)

Отыскание кратчайшего пути (методом Дейкстры):

Построение максимального потока и отыскание минимального сечения в заданной транспортной сети:

Задача об оптимальном назначении:

Фрагменты семинара от 24 мая (подготовка к контрольной работе №2)

Задача об оптимальном назначении. Пример с "расчеркиванием" выделенного элемента в матрице эффективностей:

Точное условие четырёх заданий, связанных с заданными графом и матрицей, приведено ранее.

Демонстрационная версия зачетного билета по ОДМ